Fast Fourier Transform

The Fourier Transform is a mathematical transformation which switches a set of data between the linear and spectral domains. This transformation is extremely fundamental to our reality because these two complimentary domains, or views, of a system are common to all contexts of change and are at the heart of such complex problems as the wave-particle duality and the uncertainty principle.

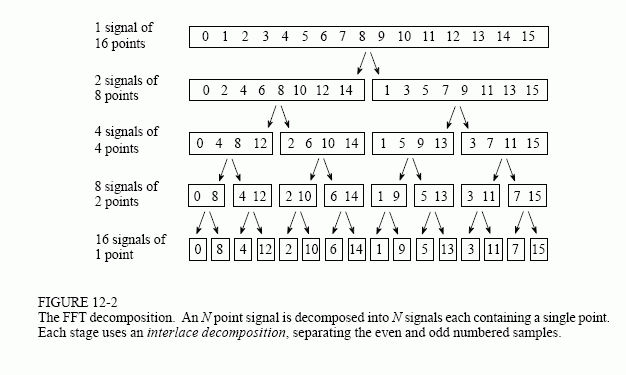
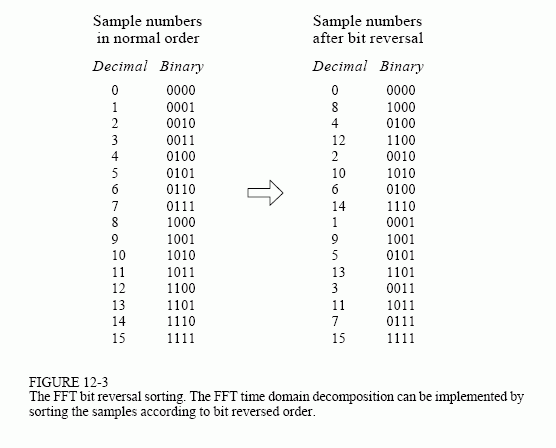
One flavour of Fourier transform is the Fast Fourier Transform (FFT) which has been optimised from square to logarithmic efficiency by taking advantage of the fact that the process is essentially binary in nature. For a detailed description of how the FFT works, see http://www.dspguide.com/ch12/2.htm.

The two diagrams below are from http://www.dspguide.com/ch12/2.htm and reveal a fundamental principle of how the linear and spectral are tied together at the most basic discrete level. The binary counting process (of stringing binary digits together to form a "number") yields a potentially infinite sequence of items and a simple geometric process allowing any one to be changed to the successive or previous item.

If we consider a binary sequence as being able to be read from left to right, or from right to left, and that each binary sequence represents a specific point on a line, then as can be seen from the diagrams below, the pattern formed by iteration through the sequence when reading them backwards is perfectly multiplexed - i.e. we have the geometry of parallel computation where time is evenly distributed across the whole space at the same time, rather than starting at one end and moving to the other over time. See The two domains.

In terms of Nodal Reduction this multiplexed pattern is the same order that nodes would be executed in a four-layer nodal structure where each node contains a loop of two nodes.

Relation to Quantum Mechanics

In quantum mechanics the momentum and position wave functions are Fourier transform pairs to within a factor of Planck's constant.

See also

• Binary traversal
• Fourier transform
• The two domains
• Hilbert space
• Chinese remainder theorem - Some weird theorem to do with modulo arithmetic closely related to multiplexing from 300AD
• Vitalik Buterin talks about FFT
• 3Blue1Brown video explaining the Fourier transform formula
• Fourier transforms with analogue computers