SWF e-book

SWF e-book.xml|set-publish.xml|swf.php

SWF e-book.xml|swf.php|nowiki.php

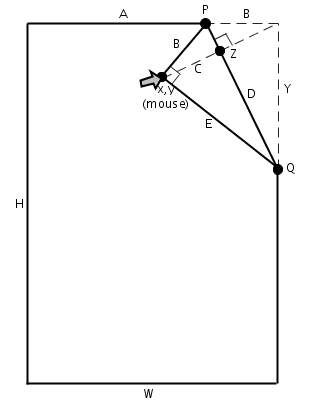
• The foundation of the effects can be built from resolving points P and Q
• P and Q are obtained from the intersections of the top and right page edges with line D
• Line D is perpendicular to line C and passes through point Z which is the midpoint of line C
• Source code is SWF e-book.as

Planned code

onMouseDown	set tx,ty from mouse position
onMouseUp	sets animation counter (i) if not a drag
onFrame	if animating, coords = Animate(i--,tx,ty) if dragging coords = mouse position if coords were set, pageTurn(coords,tx,ty)

Current issues

Flipping the folding operation horizntally and vertically

Here's the diffs showing the changes for flipping the page-fold horizontally or vertically (middle best handled after these two)...

• TR → TL (uses Tx to flip right to left)
• TR → BR (uses Ty to flip top to bottom)

Notice that the differences can all be expressed as simple changes of sign of an item in some of the expressions. Tx is -1 or +1, Ty is -1, 0 or +1. Tx and Ty use those values so that they can be used as multipliers to either change the sign of what they multiplied with (if its -1) or leave it unchanged if its +1.

text position and rotation

The text can't be rotated while it's using device-rendering for fonts. They must be embedded, but the ming-format fonts have to be embedded from swf.php (and could later be incorporated into the associated XML articles like PNG's etc).

page-fold rendering bug

The current problem which I'll check out a bit more soon is that at a certain point moving outside the top-right of the page causes a rendering problem, it appears as a large triagular page where it should actually exit without folding at all in those scenarios. Here's a table showing the values of points P,Q,R and co-ordinates x,y and dx,dy for three cases of movement near the problem area. The first column is the working case, the second is the triangle problem which has its left most point in the books top-center, and the last column is the triangle with left point far off the left side.

P	(0,0)	(0,0)	(∞,0)
Q	(250,5)	(250,300)	(250,300)
R	(250,5)	(250,300)	(250,300)
x,y	(250,10)	(0,<1)	(250,0)
dx,dy	(0,10)	(250,<1)	(0,0)