Difference between revisions of "Example nodal structures"
m (Caretaker: categories) |
m (Caretaker: nodal-directions) |
||
| Line 11: | Line 11: | ||
= Nodal loops = | = Nodal loops = | ||
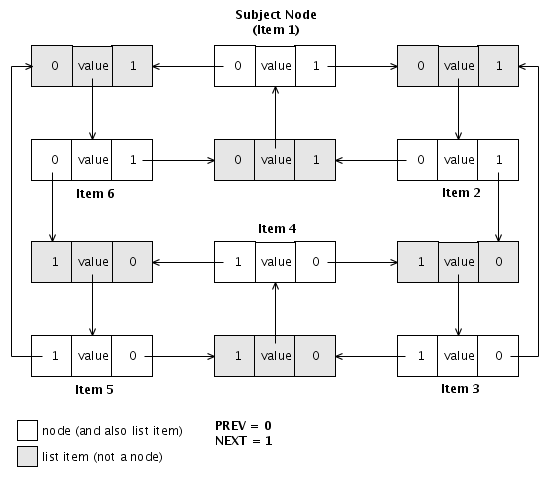
| − | This is example shows a complete [[loop]] of six [[node]]s made from | + | This is example shows a complete [[loop]] of six [[node]]s made from {{right}} and {{left}} nodal [[association]]s. The ''NEXT'' and ''PREV'' are the first two [[binary traversal|traversable]] node indexes which translate to the two single-bit paths. |
[[Image:loop.png]] | [[Image:loop.png]] | ||
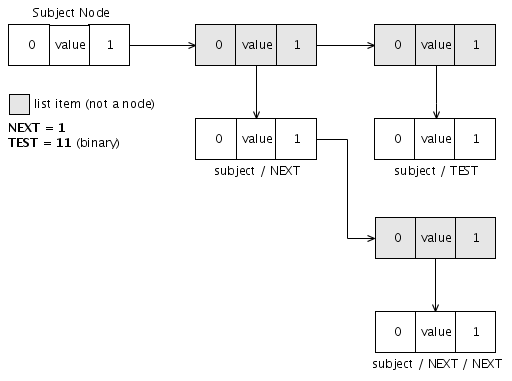
| − | This example shows how a single path of two successive 1's (called TEST in this example) doesn't conflict with two successive | + | This example shows how a single path of two successive 1's (called TEST in this example) doesn't conflict with two successive {{right}} (1) [[binary traversal|traversals]]. It's because traversal is a [[list space]] operation, but [[loop]]s are formed from [[association]]s in [[node space]]. |
[[Image:Nodal-loop-example1.png]] | [[Image:Nodal-loop-example1.png]] | ||
Revision as of 16:29, 27 February 2007
About the diagrams
Nodes and list-items: All nodes are list items in a list space (a node space is a subset of a list space), this distinction has been indicated in the diagrams by making the nodal-list-items white and the non-nodal-list-items gray.
Arrows: All list-items are composed of three list item keys which are each an index to another list-item. Note that the indexes refer to an entire list item of three keys, not to an individual key within an item. The arrows in the diagrams show this by the start points being inside one of the list-item-keys, but the end point connects to the edge which is common to all three keys. So all arrows point from a list-item-key to a list-item.
This is an article for discussing and displaying various nodal structures and examples. These diagrams are being made online with Gliffy, login with email address aran@organicdesign.co.nz and password project to modify or create new nodal diagrams.
[[+Gliffy/Collaboration|]]
Nodal loops
This is example shows a complete loop of six nodes made from Right and Left nodal associations. The NEXT and PREV are the first two traversable node indexes which translate to the two single-bit paths.
This example shows how a single path of two successive 1's (called TEST in this example) doesn't conflict with two successive Right (1) traversals. It's because traversal is a list space operation, but loops are formed from associations in node space.