Difference between revisions of "Quantum computation"
m (Quantum computer moved to Quantum computation) |
(quantum conputation and brains functions) |
||
| Line 1: | Line 1: | ||
| + | Computers have multiplied by millions of times in their power over the last decades, but still there are many areas in which they seem to have not gained much in power, for example they still seem light years away from being able to understand spoken language or learning and applying new concepts. At first it was thought to be a lack of computational power or a lack of understanding of the neural network systems our brains employ to do such learning. But nowadays our computers are far more powerful than any single brain and neural networks are understood well and shown not to be [[w:Turing machine|turing machines]] - they do not perform any operations that can't be performed by any other computational machine of sufficient power. | ||
| + | |||
| + | It turns out that this class of computationally insurmountable problems which brains seem to be able to perform with such ease are all expressible as [[w:Optimization problems|optimisation problems]] which treat the entire set of feasible solutions as a space like a terrain where the lowest points represent the most optimal solutions. Using classical techniques it's very difficult to know whether a low point in the space (a local ''minima'') is a comparatively good one or not without searching the entire space which is usually computationally infeasible or impossible, so many techniques such as [[w:simulated annealing|simulated annealing]] have been developed to try and find globally good minima at a practical cost. But no classical methods have been achieved which solve the difficult problems anywhere near as effectively as the brain even though the computational power is far superior. | ||
| + | |||
| + | [[Image:Quantum annealing.jpg|200px|right]] | ||
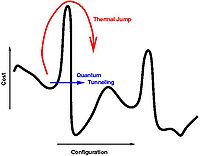
| + | Recent advances in [[w:quantum computation|quantum computation]] have shown that quantum computers are extremely proficient when it comes to solving optimisation problems. They use a process called [[w:Quantum annealing|quantum annealing]] which basically employs the [[w:Quantum tunnelling|quantum tunnelling]] effect to find successively lower minima in the solution space. | ||
| + | |||
| + | There is very strong evidence which suggests that this is the process our brains are actually using to achieve these seemingly impossible computational tasks, also many enzymes are known to use quantum tunnelling and even the anti-oxidation process used by common green tea has been shown to use the quantum tunnelling effect. In the brain, the quantum annealing process is the slow problem solving process which helps to form the neural connectivity, whereas the real-time stimulus-response side is done by the neural network. Many people learn to employ this side of their brains directly from an early age realising that there's some part of their mind which they can hand difficult problem over to and receive an insight hours or days later; it's the quantum computer in our brains which processes the tasks we put into this "too hard basket". | ||
| + | |||
== Quantum computation and encryption == | == Quantum computation and encryption == | ||
Determining the [[w:prime factor|prime factor]]s of a number is an example of a problem frequently used to ensure cryptographic security in encryption systems; this problem is believed to require [[w:polynomial time|superpolynomial time]] in the number of digits - it is relatively easy to construct a problem that would take longer than the known age of the Universe to calculate on current computers using current algorithms. | Determining the [[w:prime factor|prime factor]]s of a number is an example of a problem frequently used to ensure cryptographic security in encryption systems; this problem is believed to require [[w:polynomial time|superpolynomial time]] in the number of digits - it is relatively easy to construct a problem that would take longer than the known age of the Universe to calculate on current computers using current algorithms. | ||
| Line 11: | Line 20: | ||
== See also == | == See also == | ||
| − | *[http://www.youtube.com/watch?v=I56UugZ_8DI Quantum Computing Day 1: Introduction to Quantum Computing] ''- Google TechTalk'' | + | *[http://www.youtube.com/watch?v=I56UugZ_8DI Quantum Computing Day 1: Introduction to Quantum Computing] ''- Google TechTalk by [[w:Hartmut Neven|Hartmut Neven]]'' |
*[http://www.youtube.com/watch?v=vMvC-wv1ayo Quantum Computing Day 2: Image Recognition with an Adiabatic Quantum Computer] | *[http://www.youtube.com/watch?v=vMvC-wv1ayo Quantum Computing Day 2: Image Recognition with an Adiabatic Quantum Computer] | ||
*[http://www.youtube.com/watch?v=4qAIPC7vG3Y Quantum Computing Day 3: Does an Explanation of Higher Brain Function require references to quantum mechanics] | *[http://www.youtube.com/watch?v=4qAIPC7vG3Y Quantum Computing Day 3: Does an Explanation of Higher Brain Function require references to quantum mechanics] | ||
Revision as of 22:17, 29 July 2008
Computers have multiplied by millions of times in their power over the last decades, but still there are many areas in which they seem to have not gained much in power, for example they still seem light years away from being able to understand spoken language or learning and applying new concepts. At first it was thought to be a lack of computational power or a lack of understanding of the neural network systems our brains employ to do such learning. But nowadays our computers are far more powerful than any single brain and neural networks are understood well and shown not to be turing machines - they do not perform any operations that can't be performed by any other computational machine of sufficient power.
It turns out that this class of computationally insurmountable problems which brains seem to be able to perform with such ease are all expressible as optimisation problems which treat the entire set of feasible solutions as a space like a terrain where the lowest points represent the most optimal solutions. Using classical techniques it's very difficult to know whether a low point in the space (a local minima) is a comparatively good one or not without searching the entire space which is usually computationally infeasible or impossible, so many techniques such as simulated annealing have been developed to try and find globally good minima at a practical cost. But no classical methods have been achieved which solve the difficult problems anywhere near as effectively as the brain even though the computational power is far superior.
Recent advances in quantum computation have shown that quantum computers are extremely proficient when it comes to solving optimisation problems. They use a process called quantum annealing which basically employs the quantum tunnelling effect to find successively lower minima in the solution space.
There is very strong evidence which suggests that this is the process our brains are actually using to achieve these seemingly impossible computational tasks, also many enzymes are known to use quantum tunnelling and even the anti-oxidation process used by common green tea has been shown to use the quantum tunnelling effect. In the brain, the quantum annealing process is the slow problem solving process which helps to form the neural connectivity, whereas the real-time stimulus-response side is done by the neural network. Many people learn to employ this side of their brains directly from an early age realising that there's some part of their mind which they can hand difficult problem over to and receive an insight hours or days later; it's the quantum computer in our brains which processes the tasks we put into this "too hard basket".
Quantum computation and encryption
Determining the prime factors of a number is an example of a problem frequently used to ensure cryptographic security in encryption systems; this problem is believed to require superpolynomial time in the number of digits - it is relatively easy to construct a problem that would take longer than the known age of the Universe to calculate on current computers using current algorithms.
Shor's algorithm is a quantum algorithm for integer factorization. On a quantum computer, Shor's algorithm takes time O((log N)3) to factor an integer N. This is exponentially faster than the best-known classical factoring algorithm, which works in time about [math]O(2^{{(\log N)}^{1/3}})[/math]. Peter Shor discovered the eponymous algorithm in 1994.
Shor's algorithm is important because it breaks a widely used public-key cryptography scheme known as RSA. RSA is based on the assumption that factoring large numbers is computationally infeasible. So far as is known, this assumption is valid for classical computers. No classical algorithm is known that can factor in time polynomial in log N. However, Shor's algorithm shows that factoring is efficient on a quantum computer, so a quantum computer could "break" RSA.
A way out of this dilemma would be to use some kind of quantum cryptography. There are also some digital signature schemes that are believed to be secure against quantum computers. See for instance Lamport signatures.
Grover's algorithm can also be used to obtain a quadratic speed-up [over a brute-force search] for the NP-complete class of problems.