Difference between revisions of "Quantum computation"
m (→Quantum computation and encryption) |
m (→See also) |
||
| Line 33: | Line 33: | ||
*[http://www.youtube.com/watch?v=vMvC-wv1ayo Quantum Computing Day 2: Image Recognition with an Adiabatic Quantum Computer] | *[http://www.youtube.com/watch?v=vMvC-wv1ayo Quantum Computing Day 2: Image Recognition with an Adiabatic Quantum Computer] | ||
*[http://www.youtube.com/watch?v=4qAIPC7vG3Y Quantum Computing Day 3: Does an Explanation of Higher Brain Function require references to quantum mechanics] | *[http://www.youtube.com/watch?v=4qAIPC7vG3Y Quantum Computing Day 3: Does an Explanation of Higher Brain Function require references to quantum mechanics] | ||
| − | *[[w: | + | *[[w:Timeline of quantum computing|Timeline of quantum computing]] |
Revision as of 07:57, 30 July 2008
Computers have multiplied by millions of times in their power over the last decades, but still there are many areas in which they seem to have not gained much in ability, for example they still seem light years away from being able to partake in spoken conversation or learn and apply new concepts. At first it was thought to be a lack of computational power or a lack of understanding of the neural network systems our brains employ to do such tasks. But nowadays even home computers are far more powerful than any brain and neural networks are understood well and shown to be Turing machines - they do not perform any operations that can't be performed by any other computational machine of sufficient power.
It turns out that this class of computationally insurmountable problems which brains seem to be able to perform with such ease are all expressible as optimisation problems, which basically arrange the entire set of feasible solutions into a "landscape" where the lowest points represent the most optimal solutions. Using classical techniques it's very difficult to know whether a low point in the space (a local minima) is a comparatively good one or not without searching the entire space which is usually computationally infeasible or impossible, so many techniques such as simulated annealing have been developed to try and find globally good minima at a practical cost. But no classical methods have been achieved which solve the difficult problems anywhere near as effectively as the brain even though the computational power is far superior.
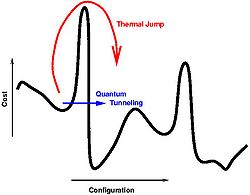
Recent advances in quantum computation have shown that quantum computers are extremely proficient when it comes to solving optimisation problems. They use a process called quantum annealing which basically employs the quantum tunnelling effect to find successively lower minima in the solution space. Usually quantum tunnelling applies to confined particles which can escape confinement by taking advantage of the Heisenburg uncertainty principle which allows them to have a probability of existing outside their confined area. In a quantum computer, this affect can be applied to the current point of focus in a search space rather than to a particle in physical space. The diagram to the right gives you the basic idea.
There is very strong evidence which suggests that this is the process our brains are actually using to achieve these seemingly impossible computational tasks, also many enzymes are known to use quantum tunnelling and even the anti-oxidation process used by common green tea has been shown to use the quantum tunnelling effect. In the brain, the quantum annealing process is the slow problem solving process which helps to form the neural connectivity, whereas the real-time stimulus-response side is done by the neural network. Many people learn to employ their quantum side from an early age, realising that there's an aspect of their mind which they can hand difficult problems over to and receive deep insight back from it hours or days later; it's the quantum computer in our brains which processes the tasks we put into this "too hard basket".
Quantum chips
Rather than having a dedicated "quantum computer" as such, the more likely way that the technology will develop is in the form of co-processor chips which would form a part of the existing computers or chips. This is because quantum computation is not very good a normal computation, it only really specialises in solving the problems which can be expressed as a specific class of optimisation problems as described above.
The chips being developed now, such as the 28-qubit adiabatic chip developed by D-Wave Systems shown to the right, are not powerful enough to be of real use in practical applications and are solely being used for research and development of further quantum computing technology.
When the technology is mature, computers will most likely exhibit a dedicated quantum chip, or perhaps future CPU's will exhibit quantum cores in addition to their standard processing cores. Computers equipped with such technology should be vastly different in usability from our current ones, for starters we should be able to converse with them as we would any other human thereby requiring only minimal use of a keyboard and mouse.
This would be far more than simple voice recognition, it brings actual understanding of the conversation by the computer into the realm of feasibility. Imagine a day when you could say high level things to your computer like, "computer, could you please invite my friends over for drinks on Friday next week? and if anyone hasn't responded by Wednesday send a reminder".
Quantum computation and encryption
Determining the prime factors of a number is an example of a problem frequently used to ensure cryptographic security in encryption systems; this problem is believed to require superpolynomial time in the number of digits - it is relatively easy to construct a problem that would take longer than the known age of the Universe to calculate on current computers using current algorithms.
Shor's algorithm is a quantum algorithm for integer factorization. On a quantum computer, Shor's algorithm takes time O((log N)3) to factor an integer N. This is exponentially faster than the best-known classical factoring algorithm, which works in time about [math]O(2^{{(\log N)}^{1/3}})[/math]. Peter Shor discovered the eponymous algorithm in 1994.
Shor's algorithm is important because it breaks a widely used public-key cryptography scheme known as RSA. RSA is based on the assumption that factoring large numbers is computationally infeasible. So far as is known, this assumption is valid for classical computers. No classical algorithm is known that can factor in time polynomial in log N. However, Shor's algorithm shows that factoring is efficient on a quantum computer, so a quantum computer could "break" RSA.
A way out of this dilemma would be to use some kind of quantum cryptography. There are also some digital signature schemes that are believed to be secure against quantum computers, such as Lamport signatures.
Grover's algorithm can also be used to obtain a quadratic speed-up [over a brute-force search] for the NP-complete class of problems.
See also
- Quantum Computing Day 1: Introduction to Quantum Computing - Google TechTalk by Hartmut Neven
- Quantum Computing Day 2: Image Recognition with an Adiabatic Quantum Computer
- Quantum Computing Day 3: Does an Explanation of Higher Brain Function require references to quantum mechanics
- Timeline of quantum computing