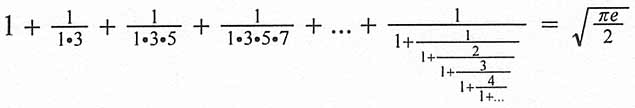Difference between revisions of "E"
m (→Factorial & the Gamma Function =) |
m (→Factorial & the Gamma Function =) |
||
| Line 24: | Line 24: | ||
<table class=document-code><tr><td>[[+phi.c]]</table> | <table class=document-code><tr><td>[[+phi.c]]</table> | ||
| − | === Factorial & the Gamma Function | + | === Factorial & the Gamma Function === |
The ''Gamma function'' extends the [[w:factorial|factorial]] function to [[w:complex number|complex]] and non-integer numbers (it is already defined on the naturals, and has [[w:simple pole|simple pole]]s at the negative integers). The Gamma function "fills in" the factorial function for non-integer and complex values of ''n''. If ''z'' is a real variable, then for natural number values only, we have | The ''Gamma function'' extends the [[w:factorial|factorial]] function to [[w:complex number|complex]] and non-integer numbers (it is already defined on the naturals, and has [[w:simple pole|simple pole]]s at the negative integers). The Gamma function "fills in" the factorial function for non-integer and complex values of ''n''. If ''z'' is a real variable, then for natural number values only, we have | ||
| Line 31: | Line 31: | ||
but for non-natural values of ''z'', the above equation does not apply, since the factorial function is not defined. | but for non-natural values of ''z'', the above equation does not apply, since the factorial function is not defined. | ||
| − | The notation Γ(''z'') is due to [[w:Adrien-Marie Legendre|Adrien-Marie Legendre]]. If the real part of the complex number ''z'' is positive, then the integral | + | The notation Γ(''z'') is due to [[w:Adrien-Marie Legendre|Adrien-Marie Legendre]]. If the real part of the complex number ''z'' is positive, then the following integral [[w:Absolute_convergence|converges absolutely]]: |
:<math>\Gamma(z) = \int_0^\infty t^{z-1} e^{-t}\,dt</math> | :<math>\Gamma(z) = \int_0^\infty t^{z-1} e^{-t}\,dt</math> | ||
Revision as of 08:43, 25 October 2006
| A page for e, i, π, and φ |
The role that the exponential function (ex) plays is extremely significant to an understanding of the laws of nature and harmonic organisation.
[math]e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots[/math]
As an infinite sum ex is Σ(xn/n!) = 1 + x / 1 + x.x / 1.2 + x.x.x / 1.2.3 + x.x.x.x / 1.2.3.4 + ...
We can look at the construction of this relation more easily by describing it by an algorithm. We can remove the power and factorial operations by basing the current numerator and denominator values on the previous values:
| +e.pl |
But a better conceptual representation is to restructure it such that the division occurs outside the main loop since its also a higher-level operation. So each iteration is now maintaining the value of a numerator and denominator which represent the entire preceeding series as a single fraction which can be reduced afterwards.
| +alt e.pl |
Here's a snipit in C which uses the taylor series of cosine to make Φ from π
| +phi.c |
Factorial & the Gamma Function
The Gamma function extends the factorial function to complex and non-integer numbers (it is already defined on the naturals, and has simple poles at the negative integers). The Gamma function "fills in" the factorial function for non-integer and complex values of n. If z is a real variable, then for natural number values only, we have
- [math]\Gamma(z+1)=z!\, [/math]
but for non-natural values of z, the above equation does not apply, since the factorial function is not defined.
The notation Γ(z) is due to Adrien-Marie Legendre. If the real part of the complex number z is positive, then the following integral converges absolutely:
- [math]\Gamma(z) = \int_0^\infty t^{z-1} e^{-t}\,dt[/math]
- See also