Sacred geometry
| There is no matter, as such. All matter exists only by virtue of a force which brings the particle of an atom to vibration and holds this most minute solar system of an atom together. We must assume behind this force, the existence of a conscious and intelligent mind. This mind is the matrix of all matter. | |
| — Max Planck |
Contents
Euclidean space
On Rn, the intuitive notion of length of the vector x = [x1, x2, ..., xn] is captured by the formula
- [math]\|\mathbf{x}\| := \sqrt{x_1^2 + \cdots + x_n^2}.[/math]
This gives the ordinary distance from the origin to the point x, a consequence of the Pythagorean theorem and the parallelogram law.
The Euclidean norm is by far the most commonly used norm on Rn, but there are other norms on this vector space as will be shown below. However all these norms are equivalent in the sense that they all define the same topology.
On Cn the most common norm is
- [math]\|\mathbf{z}\| := \sqrt{|z_1|^2 + \cdots + |z_n|^2}= \sqrt{z_1 \bar z_1 + \cdots + z_n \bar z_n}.[/math]
where [math]\bar z[/math] is the complex conjugate of z (the clockwise rotated and horizontally flipped form used in standard matrix multiplication, but with all the items being complex conjugates of the original - i.e. having the sign of their imaginary components flipped). An alternate notation for the complex conjugate is [math]z*[/math]. However, the [math]\bar z[/math] notation avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of complex conjugation. If a complex number is represented as a 2×2 matrix, the notations are identical. Also, the determinant of a square matrix is the same as that of its transpose.
In each case we can also express the norm as the square root of the inner product of the vector and itself:
- [math]\|\mathbf{x}\| := \sqrt{\mathbf{x}^{T}\mathbf{x}}.[/math] or [math]\|x\| =\sqrt{\langle x, x\rangle}.[/math]
Here [math]{x}^{T}[/math] refers to the complex conjugate of [math]{x}[/math].
The Euclidean norm measures the distance of a point to the origin of Euclidean space:
- [math]\|\mathbf{p}\| = \sqrt{p_1^2+p_2^2+\cdots +p_n^2} = \sqrt{\mathbf{p}\cdot\mathbf{p}}[/math]
where the last equation involves the dot product (a vector formed by multiplying the corresponding elements of two other vectors) with itself. This is the length of p, when regarded as a Euclidean vector from the origin. The distance itself is given by
- [math]\|\mathbf{p} - \mathbf{q}\| = \sqrt{(\mathbf{p}-\mathbf{q})\cdot(\mathbf{p}-\mathbf{q})} = \sqrt{\|\mathbf{p}\|^2 + \|\mathbf{q}\|^2 - 2\mathbf{p}\cdot\mathbf{q}}.[/math]
The Euclidean norm is also called the Euclidean length, and the L2 distance, ℓ2 distance, L2 norm, or ℓ2 norm; see Lp space. The set of vectors whose Euclidean norm is a given constant forms the surface of an n-sphere, with n+1 being the dimension of the Euclidean space.
Notes on the general structure
Every p-brane sweeps out a (p+1)-dimensional world-volume as it propagates through spacetime. The volume of an n-dimensional hypersphere can be expressed as:
[math]V_n={\pi^{n/2}R^n\over (n/2)!}.[/math]
Note that the Gamma function is required for odd dimensions and that its value cancels out the apparent fractional power of π in those cases.
Why does it cancel the fractional power? Because based on [math]\Gamma(1/2) = \sqrt{\pi}[/math], we find that the Gamma function for any half-integer can be described as:
- [math](n+1/2)!=\sqrt{\pi}\times \prod_{k=0}^n {2k + 1 \over 2}.[/math]
This allows the top and bottom π terms to reduce to a single integer power on the top.
Taylor's theorem expresses a function f(x) as a power series in x, basically because the nth derivative of xn is n!.
- Why is it that when we reduce the function down to degree-1 through differentiation it ends up as n!? --Nad 17:16, 26 Oct 2006 (NZDT)
The fundamental theorem of algebra
In mathematics, the fundamental theorem of algebra states that every complex polynomial [math]p(z)[/math] in one variable and of degree [math]n[/math] ≥ [math]1[/math] has some complex root. In other words, the field of complex numbers is algebraically closed and therefore, as for any other algebraically closed field, the equation [math]p(z)=0[/math] has [math]n[/math] roots (not necessarily distinct).
The name of the theorem is now considered a misnomer by many mathematicians, since it is an instance of analysis rather than algebra.
Algebraically closed field
In mathematics, a field [math]F[/math] is said to be algebraically closed if every polynomial in one variable of degree at least [math]1[/math], with coefficients in [math]F[/math], has a zero (root) in [math]F[/math].
What is a field?
In abstract algebra, a field is an algebraic structure in which the operations of addition, subtraction, multiplication and division (except division by zero) may be performed, and the same rules hold which are familiar from the arithmetic of ordinary numbers.
The mathematical discipline concerned with the study of fields is called field theory.
Abstract algebra and abstract structures
Abstract algebra is the field of mathematics that studies algebraic structures, such as groups, rings, fields, modules, w:vector spaces, and algebras. Most authors nowadays simply write algebra instead of abstract algebra.
The term abstract algebra now refers to the study of all algebraic structures, as distinct from the elementary algebra taught in schools, which teaches the correct rules for manipulating formulas and algebraic expressions involving real and complex numbers, and unknowns. Elementary algebra can be taken as an informal introduction to the structures known as the real field and commutative algebra.
Contemporary mathematics and mathematical physics make intensive use of abstract algebra; for example, theoretical physics draws on Lie algebras. Fields such as algebraic number theory, algebraic topology, and algebraic geometry apply algebraic methods to other areas of mathematics. Representation theory, roughly speaking, takes the 'abstract' out of 'abstract algebra', studying the concrete side of a given structure; see model theory.
Two mathematical fields that study the properties of algebraic structures viewed as a whole are universal algebra and category theory. Algebraic structures, together with the associated homomorphisms, form categories. Category theory is a powerful formalism for studying and comparing different algebraic structures.
In universal algebra, a branch of pure mathematics, an algebraic structure consists of one or more sets closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties.
Abstractly, an "algebraic structure," is the collection of all possible models of a given set of axioms. More concretely, an algebraic structure is any particular model of some set of axioms. For example, the monster group both "is" an algebraic structure in the concrete sense, and abstractly, "has" the group structure in common with all other groups. This article employs both meanings of "structure."
This definition of an algebraic structure should not be taken as restrictive. Anything that satisfies the axioms defining a structure is an instance of that structure, regardless of how many other axioms that instance happens to have. For example, all groups are also semigroups and magmas.
Groups
The unitary group U1 is the circle group. A complex number can be represented as a 2×2 matrix with real entries which stretches and rotates the points of the plane. Every such matrix has the form
- [math] \begin{bmatrix} a & -b \\ b & \;\; a \end{bmatrix} [/math]
where a and b are real numbers. The sum and product of two such matrices is again of this form, and the product operation on matrices of this form is commutative. Every non-zero matrix of this form is invertible, and its inverse is again of this form. Therefore, the matrices of this form are a field, isomorphic to the field of complex numbers. Every such matrix can be written as
- [math] \begin{bmatrix} a & -b \\ b & \;\; a \end{bmatrix} = a \begin{bmatrix} 1 & \;\; 0 \\ 0 & \;\; 1 \end{bmatrix} + b \begin{bmatrix} 0 & -1 \\ 1 & \;\; 0 \end{bmatrix} [/math]
which suggests that we should identify the real number 1 with the identity matrix
- [math] \begin{bmatrix} 1 & \;\; 0 \\ 0 & \;\; 1 \end{bmatrix}, [/math]
and the imaginary unit i with
- [math] \begin{bmatrix} 0 & -1 \\ 1 & \;\; 0 \end{bmatrix}, [/math]
a counter-clockwise rotation by 90 degrees. Note that the square of this latter matrix is indeed equal to the 2×2 matrix that represents −1. For more information see the Wikipedia complex number entry. This matrix method of representing the complex numbers comes from the Cauchy–Riemann equations.
Lies
A Lie algebra (pronounced "Lee") is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations.
A Lie algebra is a type of an algebra over a field; it is a vector space g over some field F together with a binary operation [·, ·] : g × g → g, called the Lie bracket
A Lie group is a continuous group, in the sense that the group elements have the topology of a manifold, and the group operations are continuous functions of the elements. For example, the 2×2 real invertible matrices
Cartesian coordinates
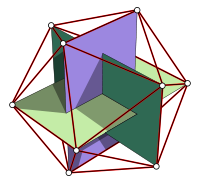
In geometry, an icosahedron, is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.
It has five triangular faces meeting at each vertex. It can be represented by its vertex figure as 3.3.3.3.3 or 35, and also by Schläfli symbol {3,5}. It is the dual of the dodecahedron, which is represented by {5,3}, having three pentagonal faces around each vertex.
The following Cartesian coordinates define the vertices of an icosahedron with edge-length 2, centered at the origin:
- (0, ±1, ±φ)
- (±1, ±φ, 0)
- (±φ, 0, ±1)
where φ = (1+√5)/2 is the golden ratio (also written τ). Note that these vertices form five sets of three concentric, mutually orthogonal golden rectangles, whose edges form Borromean rings.
If the original icosahedron has edge length 1, its dual dodecahedron has edge length [math]\frac{\sqrt{5}-1}{2}[/math], one divided by the golden ratio.
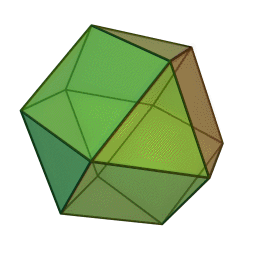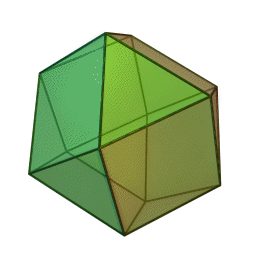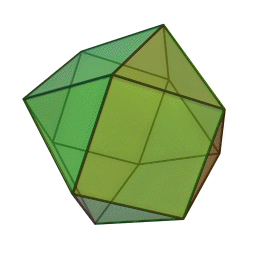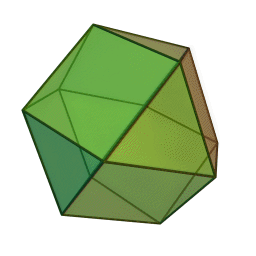
Cubeoctahedron
A cubeoctahedron also has 12 vertices, and can be defined as the intersection of two isotropic vector matrices, one inverted. Many of these images are screenshots from Nassim Haramein's lecture.

|

|
|
| Isotropic Vecor Matrix | Intersection | Cubeoctahedron |
Buckminster Fuller describes the cubeoctahedron as "vector equilibrium" because it its composed of 24 equal sized vectors, 12 pointing out from the centre and 12 on the edges all cancelling each other out in the same way a hexagon does in two dimensions. The cubeoctahedron can also be described as 8 inward-bound tetrahedrons.
 |

|
Another 24 tetrahedrons must be added to the existing 40 composing the two isotropic vector matrices to ensure that the entire structure is in equilibrium. This is now a fractal structure because the newly added 24 tetrahedra form a larger cubeoctahedron exactly twice the size of the inner one and exactly the same angle.
 |
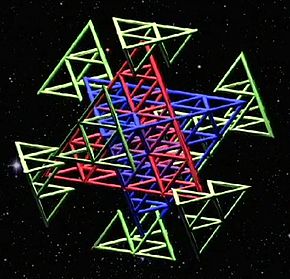
|
Black holes
There are four known, exact, black hole solutions to Einstein's equations, which describe gravity in General Relativity. Two of these (the Kerr and Kerr-Newman black holes) rotate. It is generally believed that all black holes will eventually be similar to a stationary black hole and, by the no hair theorem, that stationary black holes can be completely described by three (and only three) quantities:
- mass M,
- angular momentum J,
- electric charge Q.
This is because anything happening inside the black hole horizon cannot affect events outside it.
In terms of these properties, the four types of stationary black holes can be defined as follows:
| Stationary (J = 0) | Rotating (J > 0) | |
| Uncharged (Q = 0) | Schwarzschild | Kerr |
| Charged (Q ≠ 0) | Reissner-Nordström | Kerr-Newman |
Everything in the universe rotates, so it is not very likely that Schwarzschild black holes exist. The rotation of the black hole warps space-time so as to create two event horizons. If an object were to be sucked into a Schwarzschild black hole, there would be no way to avoid the singularity. When the object reaches the singularity it is crushed to infinite density and zero volume, and the object's mass is added to the black hole.
In the case of rotating black holes however, it is possible to avoid the singularity. A mass entering the black hole must match the direction and the velocity of the black hole's rotation. In doing this, it will be possible to "swirl" around the lethal singularity and exit the black hole in a different part of space-time. It may seem absurd that the star-ship can exit the black hole itself, however the rotating black hole distorts space-time so that the singularity can be avoided and the object can exit the black hole at reasonable speeds.
We're inside a black hole
The Schwarzschild radius of a system determines the minimum radius it can occupy without collapsing into a gravitational singularity. The Schwarzschild radius is calculated as follows:
- [math]r_s = \frac{2Gm}{c^2},[/math]
where:
- [math]r_s\![/math] is the Schwarzschild radius
- [math]G\![/math] is the gravitational constant of 6.67428 × 10−11 m3/kg/s2
- [math]m\![/math] is the mass of the gravitating object
- [math]c\![/math] is the speed of light, or 299,792,458 m/s
Substituting 1.59486 × 1055 Kg for m which is the current estimate for the mass of the universe gives us a value of 2.36 × 1028 m for the Schwarzschild radius. Even the large estimates for the size of the universe (7.38 × 1026 m) are much smaller than this which indicates that we're inside a black hole.
Sacred geometry links
- Sacred Geometry Explained - part 1 - excellent short youtube video
- Sacred Geometry Explained - part 2
- Sacred Geometry Explained - part 3
- Spirit Science
See also
- Conceptual Space
- Space & Time
- Reciprocal System of Theory
- The Thrive Movement's Code page - The code may be our most powerful key to thriving.
- The Resonance Project - Nassim Haramein's project
- e
- Hilbert space
- The privileged character of 3+1 spacetime - only 3+1 or 1+3 (space-time or time-space) are workable
- Both 3-space and 3-time exist
- On the dimensionality of spacetime - more in-depth look at the 3+1 aspect
- Radiation Rings Hint Universe Was Recycled Over and Over
- Ray Tomes - Harmonic theory of the Universe
- Symbols of Power - Adinkras and the Nature of Reality by S. James Gates
- Chestahedron - a seven-sided platonic-like solid